Tutti i pensierini.

Pensierino di Pasqua 2023

Gli stornelli di ChatGPT

Meno di un anno fa (molto o poco tempo, visto che tutto è relativo, comunque prima dello scoppio del "caso" chatGTP) mi ponevo oziose questioni sul tema dell'intelligenza artificiale, come testimoniato in questo pensierino del giugno scorso, che rileggendolo riscriverei tal quale. Trattava l'influenza della I.A. sulla struttura mentale delle prossime generazioni. Qui voglio affrontare un tema più generale, e forse, anzi sicuramente, più grande di me. Rinnovo quindi l'invito a chi queste cose le sa meglio di me di essere clemente e perdonarmi errori men che sesquipedali dovuti a volte a necessità divulgativa, più spesso ad ignoranza personale.

Credo stiamo vivendo un momento di rottura, di quelli che nella teoria del caos e delle catastrofi si chiamano punti di crisi: momenti in cui i ripiegamenti spaziotemporali portano l'Universo che conosciamo in stati di equilibrio instabile, momenti in cui l'arte della previsione del futuro - sempre aleatoria ed incerta - affronta i picchi massimi dell'incertezza e dell'aleatorietà. Essendo un tema complesso non può naturalmente essere esplicitato in due parole, e necessita di ragionamenti e conoscenze di base senza le quali tutto ciò che scriverò potrebbe sembrare balzano ed estemporaneo. Perciò mi perdonerete se faccio qualche premessa per poi esporre le tesi che voglio condividere.

Parliamo dapprima di scienza, di determinismo, di non determinismo, di indecidibilità o impredicibilità, della teoria del caos, del Nobel a Parisi, del gioco della vita, degli stornelli romani e dell'emergenza(!). Per arrivare solo alla fine di questo percorso a quello che mi preme esprimere, e che riguarda il software, la sua attuale situazione ed il punto di svolta cui stiamo arrivando. L'intelligenza artificiale è un caso particolare, in qualche modo la punta dell'iceberg che sta spuntando, quella che noi vediamo senza soffermarci su ciò che c'è sotto, che come il Titanic insegna può essere molto più inaspettato e micidiale. Farò questo percorso cercando di accompagnare per mano chi mi legge: le persone che in qualche modo mi vogliono bene e mi stimano, che sono nella loro maggioranza digiune di questi argomenti ancora più di me che ne so pochissimo.

Partiamo come sempre da lontano, con la scienza e il determinismo. Dall'età classica (Egitto, Roma ed Atene) in cui le scienze teoriche come la matematica e la filosofia, senza mai "scadere" nel settore vile e plebeo della tecnica, avevano comunque posto le basi per le scienze moderne. Poi arrivò il Medioevo, coi suoi secoli bui, gli amanuensi miniatori e la pedissequa ricopiatura degli scritti di Aristotele e delle sue spesso fallaci argomentazioni, prese per oro colato. Aristotele era un grande filosofo, ma filosofeggiava un po' troppo, e a volte aveva troppa fiducia nella propria testa e poca nella realtà dei fatti, come ad esempio quando affermava che un oggetto cade dall'alto tanto più velocemente quanto più grande è il suo peso. Altre volte in effetti si guardava intorno, ma non ci capiva proprio tutto e quindi pensava (come penserebbe chiunque di noi, ma lui era un filosofo, perbacco!) che il sole girasse intorno alla terra.

Il determinismo

Nel 1600 un Italiano si mise a fare delle prove, tirò giù sassi di peso diverso dalla Torre di Pisa e affermò (dimostrandolo) che Aristotele qualche cagata l'aveva detta. Nota bene: per questo il nostro sperimentatore, che di nome faceva Galileo, venne quasi ammazzato, e salvò la pellaccia solo perchè abiurò e disse "Occhei, ciavevate ragione voi, Aristotele è un gran figo ma vi prego lasciatemi vivere ancora un po' che ciò il cannocchiale ancora da inventare ". Poi arrivò Newton e si chiese perchè la mela gli cadeva sulla testa, e se non fosse per caso che anche lui cadeva verso la mela (a noi ci sembran cazzate, ma pensate quanto queste persone fossero avanti, e come abbiano cambiato il mondo!). Non parliamo naturalmente della terra che gira intorno al Sole e non viceversa, roba da far tremare la concezione dell'Universo, della collocazione del Sole e della Luna dentro l'Universo, della Terra dentro il sistema solare e dell'Uomo dentro la terra. Tutte queste sono cose note, ma su cui conviene riflettere quando pensiamo alle nostre certezze odierne, anche se purtoppo c'è ancora chi crede che la terra sia piatta ed il sole le giri intorno.

Dopo Galileo e Newton il mondo dell'intellighenzia nobile e borghese aveva nuovi orizzonti culturali con cui trastullarsi (il popolo continuava dal canto suo ad ubriacarsi e a scopare, o quantomeno a masturbarsi, e chissà che non facesse bene). La fisica spiegava il mondo, coadiuvata dalla matematica e dall'osservazione e misurazione degli accadimenti fisici, reali ed osservabili. Una palla di ferro ad una certa altezza lasciata scorrere giù per un piano inclinato si muoveva con un moto predicibile in base a principi e leggi fisiche ed alle equazioni matematiche che le descrivevano. Si sapeva dopo quanto tempo avrebbe raggiunto la base del piano inclinato in base all'angolo di inclinazione del piano, quale sarebbe stata la velocità finale, e anche (meraviglia delle meraviglie) che la velocità finale sarebbe stata la stessa qualsiasi fosse l'inclinazione del piano, il peso della palla ed il tempo necessario per raggiungere la base... smile

Il mondo era nelle mani (anzi, nella testa) dell'uomo. Questa piccola creatura, questo animale tra gli altri animali poteva CAPIRE la natura del mondo, spiegarla, comprendere il suo funzionamento, inferire leggi valide in assoluto, interiorizzare la matematica e la sua certezza che uno più uno farà sempre due (in realtà fin qui c'erano arrivati un paio di migliaia di anni prima). L'uomo aveva compreso il legame tra i numeri e la realtà, ed il fatto che le equazioni matematiche ci dicono come si comporta la natura, e poteva verificarlo con misurazioni, esperimenti, osservazione. La scienza ci ha fatto capire che siamo in grado di predire il futuro: Se lancio verso l'alto una palla di peso X in una direzione Y con una velocità di partenza Z posso predire esattamente dove cadrà (purtropo le innovazioni ideali arrivano spesso dalla guerra o dalla sua simulazione, come in questo caso dove la palla era di cannone; ma poco importa per questo trattatello scherzoso). Banale o incredibilmente sorprendente, quasi magico? Fate vobis. Di sicuro, una rivoluzione per l'umanità.

Insomma, illuminismo = certezze. L'uomo è al centro dell'Universo, ed è in grado di capirlo in maniera completa. I dettagli arriveranno pian piano, è chiaro che c'è sempre da andare avanti, ma di una cosa siamo sicuri: se sappiamo che 1+1 fa sempre 2, se sappiamo dove cadrà la palla di cannone, allora siamo in grado di comprendere, capire e predire tutto. Ci sono equazioni matematiche che descrivono il moto dei corpi, e anche quando scopriamo che una palla di ferro non è un oggetto fisico singolo, perchè costituita da un numero enorme di "palline" più piccole che chiamiamo atomi, poco male: il problema viene solo spostato. Infatti sapendo come si comportano gli atomi saremo in grado di inferire come si comporta la palla di ferro, semplcemente facendo la somma dei comportamenti di un numero molto grande di elementi singoli (o no?). Se conosciamo posizione e velocità di ogni particella atomica nel momento X possiamo predire esattamente dove sarà tra un po' di tempo, grazie alle equazioni che descrivono il moto.

Questo, in fisica ed in filosofia (che della fisica è ad un livello leggermente più alto, ma solo in quanto si pone il problema di che cosa sia la fisica, e per questo Aristotele ne scrisse dopo aver scritto di fisica, e venendo dopo gli scritti di fisica viene talvolta appellata metafisica) si chiama determinismo. Nota bene: per come l'ho descritto potrebbe sembrare un concetto da fisici e matematici. Potrebbe essere definito in maniera più o meno rigorosa come: se ammettiamo che il mondo sia fatto da particelle elementari (quasiasi esse siano: atomi, neutroni, quark, elettroni, muoni, adroni, co... - no, quella è un'altra cosa! - o quelchevipare), allora conoscendo posizione velocità e direzione di ogni singola particella ad un istante X posso predire dove si troverà dopo qualche secondo, e considerando tutti gli scontri che avrà con le altre particelle, cosa che so descrivere perchè obbediscono a leggi matematiche, anche dopo qualche ora. Estendendo i concetto, il futuro dell'Universo, dal raffreddore del rabbino israelita sulle pendici del monte Sinai nel 2050 alla morte del paramecio nella Fossa delle Marianne per l'incontro con una medusa di profondità nel 2130 saranno eventi prevedibili, in qualche modo già scritti nel grande Libro del Tempo.

Determinismo. Bello, no? ...Certo, non abbiamo tutte le informazioni necessarie, solo Dio (se esiste) può conoscere in un certo istante la posizione e la velocità di tutte le particelle elementari del mondo, ma abbiamo una certezza: se e quando lo potremo sapere anche noi, saremo come Dio, e per l'uomo il futuro non sarà più un'incognita. Tutto è stabilito, dal big bang in poi, noi non possiamo (ancora) saperlo, ma così è. Equazioni, numeri e dati possono descrivere non solo il presente, ma predire il futuro.

Questo è il determinismo. Ad alcuni potrà sembrare demenziale, ad altri assolutamente normale e banale. Questo modo di pensare ha permeato il pensiero filosofico e scientifico per oltre tre secoli, ed è ancora duro a morire. Non sto a dilungarmi sulle conseguenze filosofiche ed etiche che questa teoria si porta dietro, che peraltro sono facilmente intuibili: secondo questo modo di vedere, ad esempio, il libero arbitrio non esiste, tutto è predeterminato, nessuno ha il minimo controllo sulla propria vita perchè quello che ha fatto, che fa e che farà è stato scritto nel momento del big bang, e niente potrà mai mutarlo.

Pensando un minimo a questa visione del mondo naturalmente ci si accorge che c'è qualcosa che non va, ma non sappiamo bene dire che cosa sia. I più grandi filosofi e teologi si sono cimentati col tema del libero arbitrio e di come questo possa fare i conti con le teorie scientifiche che lo escluderebbero: più la scienza dice che l'arbitrio è limitato, più questa teoria della sua non esistenza ci sconforta e ci delude. Se qualcuno fosse interessato ad approfondire questo tema consiglio la lettura del libro di Gazzaniga in bibliografia, ma non è questo il tema del pensierino, perciò andiamo in un'altra direzione, che esclude il determinismo e che dalla fine dell'800 si è fatta strada nella filosofia della scienza e nella realtà di tutti i giorni, come vedremo. A piccoli passi, ma sempre più inesorabilmente.

La non calcolabilità

La prima a cadere è stata la fiducia cieca in ciò che la matematica può fare. Dai fasti dell'illuminismo alla realtà dei fatti: un matematico, anzi in realtà un fisico matematico (Jules-Henri Poincaré) alla fine dell'800 si rese conto che un problema piuttosto semplice non aveva affat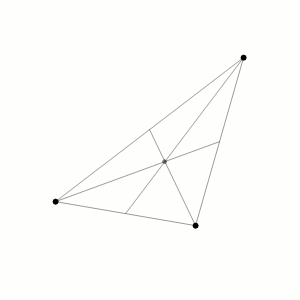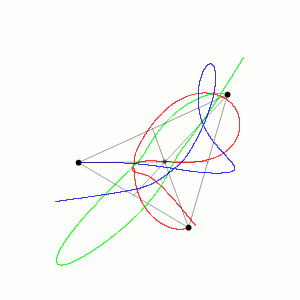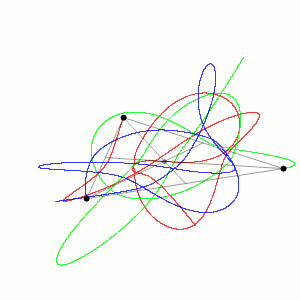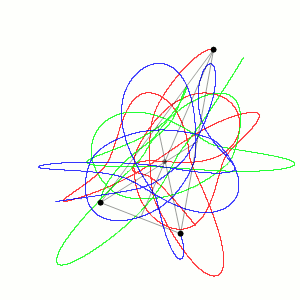tre corpito soluzioni semplici, anzi! Il problema, conosciuto come "problema dei tre corpi" prende spunto dalle equazioni dell'attrazione gravitazionale, sì proprio quella di Newton e delle mele cadenti. Matematicamente la legge è molto semplice: due corpi nello spazio si attraggono con una forza direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza che li separa: una equazione quasi banale. Infatti se i corpi sono due, con massa e distanza determinata in un certo punto dello spazio vuoto, si riesce benissimo a determinarne la traiettoria che avranno una volta lasciati liberi di muoversi.

Questo vuol dire essere in grado di predire il futuro del sistema: Se io metto nel vuoto una palla di cemento che pesa 5 tonnellate a distanza di 700 metri da una palla di piombo del peso di duecento chili posso facimente dire, risolvendo le equazioni relative, a che distanza saranno le due palle dopo undici, dodici, tredici secondi, e quali saranno le loro velocità e le loro traiettorie. Facile, no? Bè, ma Poincarè provò a fare una cosa solo leggermente più complessa: mise tre palle, di peso diverso, nello spazio, ai vertici di un triangolo scaleno, e provò a risolvere le equazioni relative, per vedere dove sarebbero state dopo undici, dodici, tredici secondi. E non ci riuscì. E da allora nessuno c'è mai riuscito. Ammazzalo, eppure sembrava facile! In fondo se tu metti quelle tre masse nello spazio e poi le lasci andare, da qualche parte vanno, no? E perchè non riusciamo a predire esattamente dove andranno? Sappiamo diverse cose del loro moto, ad esempio che il loro "centro di massa" sarà sempre lo stesso, che non andranno mai troppo lontano, che il loro moto sembrerà una leggiadra danza dalle movenze sinuose ma imprevedibili. Ma dove saranno le singole palle dopo un certo tempo non possiamo saperlo con esattezza.

Per farlo ci sono solo due modi: Uno è fare l'esperimento e vedere quel che succede, l'altro non è risolvere le equazioni differenziali che regoleranno il moto (cosa che non sappiamo fare), ma fare delle approssimazioni. Attenzione qui, perchè questo è un passaggio importante: con metodi di calcolo numerici riesco a simulare molto bene dove saranno le tre palle un decimillesimo di secondo dopo che sono state lasciate. Non lo saprò esattamente, ma con un grado di approssimazione sufficiente per tutti gli scopi pratici (un approccio ingegneristico invece che matematico, insomma). Allora se io metto le palle dove presumo saranno un decimillesimo di secondo dopo e rifaccio i conti, saprò dove saranno ancora un decimillesimo di secondo dopo (che fa due decimillesimi da quando ho iniziato a lavorare). Anche qui, ci sarà un piccolissimo errore, men che infinitesimale, e io potrò andare avanti con la simulazione. Ma se riuscirò a predire abbastanza bene dove saranno le palle dopo un secondo, purtroppo tutti questi errori infinitamente piccoli che ho fatto ad ogni passo si accumuleranno, e se andrò a vedere dove stanno le palle dopo un'ora non sarò più tanto sicuro che l'errore non sia di qualche metro. E dopo un giorno di qualche chilometro, e dopo un mese non saprò assolutamente dire dove staranno le tre palle, purtroppo... sad

I numeri primi (c'entrano poco ma c'entrano)

Pensiero estemporaneo dell'encomiabile lettore arrivato a questo punto: "Mò che succede? Questo pirla ci vuole spiegare la teoria del caos con un pensierino del menga?" Boh, non lo so se ci riesco, anche perchè non sono sicuro di averla capita bene neanch'io, ma sicuramente posso provare a spiegare quel che ho capito io...

Tirem'innanz. Siamo arrivati ad una prima evidenza con il determinismo fisico: le equazioni non sempre risolvono i problemi. Alcuni problemi sicuramente hanno una soluzione, ma l'unica maniera per trovarla è far funzionare le cose e vedere cosa capita. In un certo senso, in questo caso il futuro E' predeterminato, ma non conosciamo un'altra via per conoscerlo se non quella di aspettare e vedere che succede. Mi scuso per l'apparente banalità dell'affermazione, ma siamo ad un punto cruciale tra il determinismo e l'indeterminatezza, per cui vale la pena fare una ulteriore riflessione.

Parliamo di un argomento che tra i matematici è un classico assoluto, che ha grande importanza nella nostra vita di tutti i giorni (ad esempio quando andiamo a controllare il conto in banca in Internet e ci fidiamo che chi ce lo dice sia la nostra banca e non un truffatore che ci frega un euro al giorno) e che pochi non addetti ai lavori conoscono: i numeri primi. Il concetto di "numero primo" è assolutamente basilare e facile in matematica, ma i numeri primi sono un rebus che i matematici stentano ancora a risolvere. Se chiediamo ad una persona "pensa un numero" quello penserà un numero tra uno e cento, al massimo tra uno e mille. In questo caso, determinare se il numero pensato è primo non sarà difficile: basterà cercare in una tabellina coi primi mille numeri primi e sicuramente o lo troveremo (nel qual caso quello era un numero primo) oppure non lo troveremo, e allora a meno di un errore nella tabellina sapremo che non era un numero primo.

Ma davvero devo usare una tabellina? Non c'è modo di vedere più rapidamente se un numero è primo o no? la risposta è che un metodo più veloce non c'è. O mi faccio il conto, partendo da uno, e controllo che quel numero non sia divisibile per nessuno dei numeri che lo precedono (in realtà basta arrivare alla metà, ma se non lo capite non vi spiego il perchè gogogo ) oppure vado a vedere la tabellina, o sennò resterò col dubbio. Ma ora immaginiamo di chiedere ad una persona: pensa, o meglio, scrivi, un numero di diecimila cifre che finisca con 1,3,7 o 9. E poi pensiamo di andare a vedere se questo è un numero primo o no. Ebbene, non ci sarà modo di capirlo se non tentando tutte le divisioni per tutti i numeri primi precedenti (fino a circa la metà del numero stesso). Perchè questa cosa è importante per il discorso che sto facendo? Perchè in questo caso (tornando al discorso della predicibilità o predeterminazione o determinismo del mondo) la risposta c'è ed è univoca, e la possiamo conoscere. In questo caso quindi il futuro è già scritto, è deterministico, e tra un giorno o due anni (quando avrò fatto tutti i miei calcoli) saprò la verità, che sicuramente Dio (nel caso improbabile esista) sa già adesso. Però non ho nessuna scorciatoia per saperlo, devo aspettare e vedere cosa succede, e saprò se quel numero è primo solo dopo aver fatto tutte le prove possibili (o meglio, sensate). Questo quindi è un caso di futuro certo ma non calcolabile se non con un tempo che può essere arbitrariamente lungo. Come postilla a questo paragrafetto sui numeri primi dirò che niente vieta che domani un bravo matematico riesca a scoprire una scorciatoia, una formula matemagica che ci dica rapidamente senza dover fare tutti i conti se il numero di diecimila cifre che avevo pensato è primo o no. Ma forse è meglio augurarci che questo non succeda, visto che sennò tutti i sistemi di crittazione su cui si basa la sicurezza del Web sarebbero facilmente aggirati, e il nostro conto in banca sarebbe a serio rischio... sad

Ancora un concetto: immaginiamo una sfera di metallo molto liscio, diciamo del diametro di un metro. E una biglia di vetro ancora più liscio del metallo, del diametro di un centimetro. Mettiamo la biglia in cima alla sfera di metallo. Piazziamola con tutta l'accuratezza di cui siamo capaci esattamente sulla sommità, non un decimillesimo di millimetro più in là, sennò il ragionamento non funziona. Poi chiediamoci: da che parte cadrà la biglia? tutti noi sappiamo che nel mondo reale la biglia cadrà, sennò non sarebbe stata abbastanza liscia e rotonda, anche se nel mondo della matematica in teoria la biglia non dovrebbe muoversi di là... Ma noi sappiamo che nella realtà da qualche parte cadrà, perchè il concetto di "equilibrio instabile" è chiaro a tutti (o almeno a chi ha provato una volta a stare fermo su un trampolo solo, senza muoverlo, per più di 3 secondi).

Cadrà, ma nessuno sa dire da che parte cadrà... Qual è la differenza tra i due casi, quello delle due biglie una sopra l'altra e quello dell'enorme numero primo? In entrambi i casi, in fondo, per vedere cosa accadrà dobbiamo aspettare che accada... Ma pensiamoci un attimo: nel caso del numero primo o quel numero è primo oppure no. Anche se noi all'inizio non lo sappiamo, lui nel suo essere numero è numero primo oppure no. Se abbiamo fatto bene i conti e scopriamo che quello è un numero primo, possiamo rifarli mille volte e quel numero risulterà sempre un numero primo. Adesso torniamo alle biglie: se piazziamo la biglia piccola con sufficiente cura, e facciamo mille volte la prova, avremo mille risultati differenti, non ce ne saranno due uguali. Ricordiamoci di questo particolare, ci servirà più tardi.

Piccolo intermezzo del lettore giunto a questo punto e quasi esterrefatto dalle divagazioni: ma questo qui non doveva parlare di software e di Intelligenza Artificiale? Dove stanno queste cose? Mi pare che qui si parli di matematica, filosofia, perfino etica (vedi libero arbitrio) ma di computer e software ancora non c'è traccia... Calma, calma. Avevo detto che senza retroterra quel che vorrei dire sarebbe incomprensibile, perciò finiamo di costruire il retroterra (non uso "background" per paura del ministro culturalmente autarchico) e poi arriviamo a bombazza sul software e sull'I.A. anche se magari i più smart (ahiahiahi, multa!) tra i lettori avranno immaginato dove vado a parare... :-)

Di nuovo teoria del caos (che casino!)

Torniamo per un attimo al problema dei tre corpi, e chiariamo in che senso questo sistema è "caotico" visto che abbiamo accennato alla teoria del caos. Più propriamente si definiscono sistemi caotici quelli in cui differenze piccolissime (piccole a piacere) di condizioni iniziali comportano, nel tempo, divergenze notevoli. Tornando alla palla che rotola su un piano inclinato, se faccio 1000 esperimenti cercando di mantenere fisse le condizioni iniziali (posizione della palla, inclinazione del piano, ruvidità delle superfici etc) so per certo che ci saranno piccole ed impercettibili variazioni nelle condizioni iniziali, e quanto più sono piccole queste variazioni tanto più la posizione finale della palla sarà vicina all'esperimento precedente. Nei sistemi caotici non è così. Prendendo per esempio il problema dei tre corpi (pensate alla sua semplicità estrema rispetto, ad esempio, ad avere trenta o trecento o tremila corpi!), una differenza molto piccola nelle posizioni di partenza già dopo tre "giri di valzer" darebbe luogo ad una configurazione completamente differente. L'animazione presa da wikipedia alla voce "problema dei tre corpi" (e che ho riportato nella figura) mostra che caoticità del sistema non significa niente regole. Infatti si vede bene l'esistenza di un "attrattore" (il centro di gravità) e una periodicità di movimento, in cui i tre corpi vanno e vengono e sembrano "respirare" intorno al centro di gravità. Ma dove saranno le palle se le fotografassi tra un minuto non si può dire.

La caoticità dei sistemi naturali è naturale. Tutti hanno sentito nominare l'"Effetto farfalla", protagonista anche di un noto film, anche se pochi sano cosa sia esattamente. Eppure è molto semplice, e Wikipedia lo esprime sicuramente con un numero minore di parole di quanmandelbrot1to lo farei io: "In matematica e fisica l'effetto farfalla è una locuzione che racchiude in sé la nozione maggiormente tecnica di dipendenza sensibile alle condizioni iniziali, presente nella teoria del caos. L'idea è che piccole variazioni nelle condizioni iniziali producano grandi variazioni nel comportamento a lungo termine di un sistema". Nel mondo reale l'effetto farfalla si manifesta ad esempio nella impossibilità di fare previsioni metereologiche attendibili a lungo termine. Nel mondo puro della matematica invece (per esempio) si esprime con l'enorme variabilità di comportamento di punti molto, molto vicini ai confini dell'insieme di Mandelbrot, universalmente noto per la rappresentazione delle figure che derivano andando a "cercare" i punti dell'insieme.

OK, abbiamo più o meno smarcato tre dei cinque punti della premessa, che sono:

Ne restano solo due:

Se siete arrivati fin qui, vale la pena provare ad andare oltre.

Sistemi complessi ed "emergenza"

Quando qualcuno chiede all'ormai arcinoto fisico/matematico de noantri, Giorgio Parisi, che cosa gli abbia fatto ottenere il Nobel, lui risponde "Lo studio dei sistemi complessi". E voi penserete: "Graziarcà, si ereno sistemi semplici nu je davano er Nobbel". Ed avrete ragione solo in parte. Perchè "sistema complesso" nella sua accezione scientifico/matematica ha un significato più preciso che nell'accezione quotidiana, così come la "teoria del caos" non riguarda la situazione interna della cameretta di un sedicenne innamorato, nè la sua situazione ormonale (anche se qualche connessione ce l'ha risata).

Partiamo ancora dalla matematica, dove la complessità fece una delle sue prime apparizioni alla fine degli anni 60. E' impressionante, tra l'altro, come tutte queste cose di cui sto parlando siano "esplose" in quell'epoca: Mandelbrot è esattamente coetaneo di quest'evento, e la scoperta del DNA e del codice genetico, di cui non ho ancora parlato ma lo farò tra breve, è di pochi anni prima.

Il "gioco della vita" ("Game of Life", o più semplicemente "Life") è un divertissement inventato dal matematico inglese John Conway. In un modo di pensare estremamente schematizzato e riduzionista fino all'osso, Conway si propose di "simulare" l'evoluzione della vita in un sistema semplicissimo, governato da pochissime regole banali. Per farlo, ridusse il mondo ad una scacchiera molto grande, gli esseri viventi erano delle pedine sulle caselle della scacchiera, e la "vita" veniva regolata con generazioni successive, partendo da una arbitraria configurazione iniziale di pedine sulle caselle della scacchiera.

Le facili regole: una pedina che nelle posizioni vicine non ha nessuno, oppure ha una sola altra pedina, nella generazione successiva muore (di solitudine) e viene tolta dalla scacchiera. Muoiono e vengono tolte anche le pedine che hanno intorno a sè più di tre pedine (perchè "soffocate dalla sovrappopolazione"). Le pedine che hanno intorno a sè due o tre altre pedine sopravvivono, e rimangono sulla scacchiera per un'altra generazione. Una posizione vuota (senza pedine) sulla scacchiera, se ha intorno esattamente tre pedine ha una nascita (e quindi al giro successivo avrà una pedina). La semplificazione delle regole della vita sembra piuttosto drastica, ma è solo un gioco matematico, che però ha raccontato e insegnato molto, vediamo perchè.

Intanto il problema delle generazioni successive, data una configurazione di partenza, ricorda un pochino quello dei numeri primi: Se nella mia scacchiera metto delle pedine a caso nelle caselle e mi chiedo, ad esempio, se tra cinque generazioni una certa casella avrà una pedina oppure no, mi trovo davanti ad un problema simile a quello del numero primo da diecimila cifre: so esattamente che c'è una risposta precisa (numero primo o numero non primo, casella con pedina o casella senza pedina) ma non so predirlo con nessuna formula, l'unica possibilità è "giocare" il gioco e vedere cosa succede.

Vedere un computer che gioca a "Life" può essere divertente. Il programma che lo esegue è piuttosto semplice, chiunque con un minimo di dimestichezza di programmazione può farlo. Eppure quando si guardano i risultati grafici sullo schermo si rimane spesso affascinati. Per questo, tanti anni fa un sacco di nerd curiosi si sfiziarono a giocare a "Life" con configurazioni casuali di pedine sulla scacchiera e si accorsero di una cosa interessante. La maggior parte delle configurazioni inialianteziali ha qualche generazione di vita, e poi si estingue, cioè la scacchiera rimane vuota dopo qualche generazione. Tralascio le considerazioni etico-filosofiche su questa casualità matematica, e vado invece alla parte interessante. Alcune configurazioni iniziali non muoiono, ma danno luogo a fenomeni particolari. Alcune ad esempio "pulsano" cioè hanno una configurazione che cresce, poi diminuisce senza estinguersi, poi ricresce e così via. Altre configurazioni "viaggiano" sulla scacchiera, senza estinguersi ma spostandosi all'infinito (la più semplice di queste configurazioni è quella detta dell'"aliante" che vedete in figura). Altre ancora clonano popolazioni di pedine che poi si spostano dal centro verso la periferia, mentre la configurazione centrale continua a creare satelliti che si allontanano. Per un esempio di che cosa può succedere metterndo a caso pedine su una scacchiera e giocando a life vi linko questo filmato di youtube che se volete tutto lo spiegone lo guardate dall'inizio, io ho messo già il link alle animazioni. Lascio a voi le considerazioni del caso, che come sopra evito di fare, per introdurre invece l'ultimo concetto, quello forse più interessante, quello di "emergenza".

Emergenza!

Qundo il buon John Conway inventò il giochino non avrebbe mai pensato (almeno credo) alla possibilità che da queste regole semplicissime venissero fuori, inaspettate, figure e comportamenti come quello di un "aliante", o le configurazioni "pulsar" che sembrano respirare, o i due cannoni che si sparano contro proiettili che si distruggono a vicenda (come si vede nel filmatino di youtube). Queste configurazioni che per la nostra mente sono suggestive e ricordano altri mondi e altri sistemi (come un cuore che pulsa o un aereoplano che vola) sono "emerse" inopinatamente. Nessuno mai avrebbe potuto prevederle o immaginarle mettendo a caso pedine sulla scacchiera del gioco della vita. Breve digressione sul lessico e sulle parole. "Emergenza" per noi italiani può significare contemporaneamente due cose: l'emergere di qualcosa da qualcos'altro (ad esempio un relitto dalle profondità marine, un germoglio dalla terra, o Alien dalla pancia di Sigourney Weaver) oppure una situazione estrema di pericolo, di urgenza e di richiesta di intervento immediato. L'inglese, in questo caso più accurato di noi, ha due termini distinti: "emergence" nel primo caso, "emergency" nel secondo caso. Avevate già capito, ma quando qui parlerò di "emergenza" vorrò dire "emergence" e non "emergency" cioè qualcosa che vien fuori e non "pericolo!". Ancora con la lingua inglese, un termine che abbiamo mutuato da quella lingua perchè da noi non esiste è "serendipità" ("serendipity"). Significa trovare fortunosamente qualcosa quando magari non la si stava cercando (ad esempio un tesoro sepolto mentre vango l'orto). Scoprire la configurazione "aliante" nel gioco della vita è stato un caso di serendipità, e l'"aliante" è "emerso" inaspettato dalle semplici regole del gioco e da una configurazione iniziale casuale: nessuno mai poteva aspettarsi (o poteva predire) che avrebbe generato una cosa così particolare.

Approfondiamo ancora solo per un attimo questi due concetti, e poi andiamo a scoprire il colpevole. Quando al Giorgio nazionale viene chiesto di spiegare da dove gli sia venuta questa fregola di studiare i sistemi complessi, lui cita gli storni, uccelletti che affliggono gli automobilisti non garagemuniti dell'urbe con la loro pioggia di guano dal cieStornilo. Ma a Parisi quello che interessava non erano le sordide deiezioni dei volatili, con le loro macchie casuali sui cofani capitolini (anche se l'argomento, come forse vedremo in un prossimo pensierino, avrebbe punti di contatto). Lui pensava più aulicamente agli stormi di storni che adornano con le loro figure estemporanee i tramonti autunnali di Roma. Avete sicuramente visto anche voi queste proteiformi e mutevoli figure affascinanti, che lasciano gli osservatori col naso per aria e col fiato sospeso. Queste enormi scure amebe visive che sembrano esseri viventi "emergono" dal fatto che gli storni sono a migliaia, e le "regole" che seguono nel proprio volo sono piuttosto semplici (come quelle del gioco della vita). Chi guarda il cielo a Roma in autunno non lo fa per guardare singoli uccelli in volo, ma per rimanere affascinato dalle forme assolutamente impredicibili ma coerenti, in qualche modo "vive" che emergono dall'interazione delle singole pedine del gioco degli stormi di storni. Stessa cosa capita a chi guarda le nuvole per scoprirvi paperelle o coni gelato, dragoni sputafuoco o morbidi cuscini angelici. Non certo per guardare le innumerevoli microscopiche gocce d'acqua da cui sono composte.

Anche il tema dell'"emergenza" è relativamente moderno. Non ve lo saprei tracciare in maniera così puntuale come ho fatto con altri argomenti, ma sicuramente uno dei libri più importanti che ho letto (e che non citerò mai abbastanza) ne parlava già quarant'anni fa: si chiama "Goedel, Escher e Bach" di Douglas Hofstadter (trovate il riferimento nella minibibliografia in fondo). Le riflessioni sull'"emergenza" intesa in questo senso ci fanno capire che studiare il microscopico e osservare il macroscopico che ne deriva sono entrambe attività sane e importanti, ma che credere che capendo a fondo il microscopico possiamo capire o predire o anticipare il macroscopico che ne deriva è un'illusione, e dobbiamo arrenderci a questa realtà.

Ma allora a che cosa serve studiare i sistemi complessi, se tanto non riuscirò mai a comprenderli? Perchè Parisi con le sue riflessioni, le sue intuizioni ed i suoi calcoli e impegno merita un premio? Perchè studiare la meteorologia, che unisce un sistema dalle regole semplici ma estremamente complesso come quello dell'ecosistema terrestre alla famigerata teoria del caos? Perchè andare a misurare il vento e l'umidità e le precipitazioni e la temperatura in milioni di punti, se tanto non ne verremo mai a capo? Perchè tutto è relativo, ma su questo torneremo in un prossimo pensierino, se e quando ne avrò voglia, adesso è il momento di introdurre il tema dei codici, del software e dell'Intelligenza Arificiale.

Non prima di aver citato al volo, come fosse una cosa poco importante, che tutti noi esseri viventi siamo organismi che nascono, crescono, agiscono, si riproducono e (purtroppo) muoiono sotto la guida di un codice software scritto nel DNA (programmi diversi ma scritti nello stesso linguaggio software, nota bene, per tutti gli esseri viventi, dai virus alle amebe, dai licheni alle vespe, dai pappagalli all'uomo). In questo senso il tema dei codici e della loro influenza sulla vita è vecchio quanto la vita stessa, ma era rimasto sconosciuto fino a pochi anni fa. Ancora una volta, più o meno in contemporanea, si sviluppò la logica che avrebbe portato ai computer e ai programmi software e si scoprì il codice genetico del DNA, che regola la vita sulla terra.

Il Software, nato deterministico. Lo è ancora?

Anche il software è un tema molto moderno. Anticipato negli anni 40-50 nelle sue elucubrazioni astratte (che personalmente non ho mai capito fino in fondo) da Alan Turing, noto alle cronache popolari per aver decrittato codici segreti nazisti, il tema del Software si è sviluppato letteralmente sotto i miei occhi, durante la mia vita professionale, e perciò credo di aver titolo a dire qualcosa. Nella compressione temporale e nell'accelerazione turbinosa profetizzata dalla legge di Moore il software ha ripercorso i passi della storia scientifica della matematica e della fisica degli ultimi 400 anni, evolvendo in maniera simile in un tempo all'incirca dieci volte più corto.

Quando scrivevo programmi Fortran sulle schede perforate per i mainframe IBM o Siemens, programmi Fortran o Pascal per i minicomputer PDP11, istruzioni Basic o Assembler per il Commodore 64 ero (si parva licet) come Galileo o Newton: sapevo di avere il controllo della situazione ed ero in grado di prevedere esattamente quello che sarebbe risultato dal mio lavoro. Il codice che scrivevo, compilavo e "facevo girare" avrebbe prodotto risultati prevedibili e previsti, che io conoscevo in anticipo. Già allora, e sempre di più, naturalmente, il software non era un'attività di creazione individuale ma collettiva, ognuno usava (anche se spesso con molta fatica) pezzi di software fatti da altri, assemblandoli e componendoli in programmi dalle funzionalità più complesse, ma la complessità di un programma software poteva comunque essere dominata da uno o pochi individui che lo avevano scritto e lo conoscevano.

Poi la complessità (sì, proprio intesa nel senso "parisiano" del termine) di questi sistemi ha cominciato a crescere in maniera esponenziale e a velocità vertiginosa, secondo me a causa della convergenza di quattro fattori:

Il numero, la pervasività, l'interconnessione di questi oggetti, l'interazione dei loro codici e delle basi dati su cui questi agiscono sono ormai, di fatto (e sfido chiunque a dimostrarmi il contrario) un sistema complesso come e più degli stormi di storni, del quale possiamo conoscere anche bene le regole di funzionamento di base ma che è già oggi diventato più grande della somma delle sue singole componenti. Pensate a un termitaio. Con la sua dimensione, struttura, robustezza, funzionalità emerge dal comportamento di esseri minuscoli con un sistema neurale che ormai può essere simulato, appunto, da un telefonino. Eppure nessuno mai potrebbe prevedere che mettendo insieme delle termiti si genererebbe, "emergerebbe" la struttura di un termitaio. Adesso torniamo ai telefonini, ai modem, alle smarTV, ai personal computers. Il loro numero ormai si conta a miliardi, e sono connessi e comunicano. Una grande nuvola di oggetti semiintelligenti che obbediscono a regole relativamente semplici, ma la cui interazione può risultare in qualcosa di nuovo e inaspettato, facendo "emergere" qualcosa che nessuno sospetterebbe o potrebbe mai prevedere, e che prima o poi lascerà tutti con la bocca spalancata e gli occhi affascinati, come gli storni in un tramonto romano.

In fondo è già successo proprio col caso chatGPT, anche se in maniera per il momento solo abbozzata ed embrionale, tanto che ha suscitato da un lato il dileggio dei sapientoni (che dicono che tanto è tutto un bluff e noi semo comunque mejo) e dall'altro l'anatema dei conservatori, che presi dal panico del progresso che non si sa dove ci porterà ergono mura e baluardi, leggi e divieti per fermare il nuovo che avanza. Il "caso" chatGPT ci ha messo in maniera improvvisa, inaspettata, di fronte al fatto compiuto. L'applicazione di regole software in fondo non complesse, combinate con meccanismi che simulano il funzionamento del cervello (le famigerate reti neurali), in un numero di moduli sempre crescente ed interagendo con basi dati sconfinate ha sorpreso un po' tutti. Inclusi (secondo me, e anche se non lo ammetteranno mai) quelli che il sistema lo hanno pensato, progettato e realizzato. L'Intelligenza Artificiale di ChatGPT è, sempre secondo me, solo il primo segnale dell'"emergenza" dai nuovi enormi assembramenti di sistemi software di qualcosa che è più grande e più strano e più complesso dei suoi singoli costituenti e delle formule che ne regolano le interazioni.

Allo stesso modo in cui studiare le formiche dell'Amazzonia nel funzionamento dei loro apparati cerebrali piuttosto semplici non ci avrebbe fatto prevedere che la loro interazione potesse concretizzarsi in ponti viventi costruiti dalle singole formiche per attraversare ruscelli. Allo stesso modo in cui studiare accuratamente le termiti e la loro struttura neurale non ci farebbe mai predire l'architettura dei loro termitai. Così anche noi, pur conoscendo a menadito le regole ed i singoli componenti hardware e software, che peraltro abbiamo noi stessi progettato e costruito, tra qualche tempo ci potremmo trovare di fronte a qualcosa che ci farà esclamare: "Però, chi lo avrebbe mai detto?"

FG

Post Scriptum: avevo intenzione di parlare di altri argomenti affascinanti e connessi, come il principio di indeterminazione di Heisenberg o il gatto di Scroedinger, ma ho già sbrodolato troppo. Pisciare fuori dal vaso un po' va bene, ma est modus in rebus (che significa: c'è sempre un modo di risolvere gli indovinelli) risata

Non è finita qui: scrivendo il pensierino ho pensato e scritto anche un raccontino di fantascienza, sull'onda degli argomenti di cui sopra, e pensando ai fantasmi che tormentano l'amico Valerio, che mi ha prospettato scenari del genere Diverso tempo fa. Prima ancora che io pensassi alla possibile "emergenza" di una qualche forma di "volontà" (direi "self-consciousness" se non temessi gli strali dell'autarca linguistico attualmente al potere) da questo magma di macchine, applicazioni e dati interconnessi.

Il raccontino lo trovate nella appostita sezione dei racconti, esattamente qui.

Bibliografia:

Douglas Hofstadter: Goedel, Escher, Bach: Un'Eterna Ghirlanda Brillante (Adelphi)

Douglas Hofstadter: L'io della mente (Adelphi)

Marcus du Sautoy: L'enigma dei numeri primi (Rizzoli)

Michael Gazzaniga: Chi comanda? Scienza, mente e libero arbitrio (Codice)

Giorgio Parisi: In un volo di storni (Rizzoli)

Giorgio Parisi, Piergiorgio Paterlini: Gradini che non finiscono mai (La nave di Teseo)